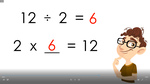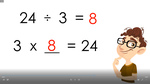Mathematics – United States – Common Core State Standards
3.OA – Operations & Algebraic Thinking
Mathematics
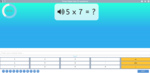
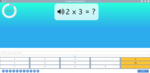
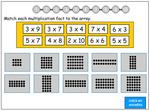
3.OA.1 – Interpret products of whole numbers, e.g., interpret 5 × 7 as the total number of objects in 5 groups of 7 objects each. For example, describe a context in which a total number of objects can be expressed as 5 × 7.
-
18 learning outcomes – click to view
Samples: Groups of 2. Groups of 5. Groups of 10. Counting on number line (by 2's). Counting on number line (by 5's).
-
Groups of two
- Activities: 4 course, 7 extra
-
Groups of five
- Activities: 5 course, 14 extra
-
Groups of ten
- Activities: 5 course, 6 extra
-
Counting on by two on a number line
- Activities: 7 course, 5 extra
-
Counting on by five on a number line
- Activities: 6 course, 3 extra
-
Counting on by ten on a number line
- Activities: 6 course, 5 extra
-
Arrays
- Activities: 4 course, 0 extra
-
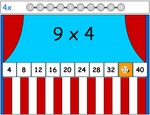
2x tables
- Activities: 12 course, 6 extra
-
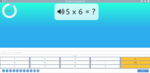
5x tables
- Activities: 9 course, 7 extra
-
10x tables
- Activities: 9 course, 6 extra
-
2x tables (problem solving)
- Activities: 2 course, 7 extra
-
5x tables (problem solving)
- Activities: 2 course, 6 extra
-
10x tables (problem solving)
- Activities: 2 course, 5 extra
-
Number patterns and groups (of 3)
- Activities: 3 course, 1 extra
-
3x tables (problem solving)
- Activities: 3 course, 3 extra
-
Groups and rows of 4
- Activities: 3 course, 4 extra
-
4x tables (problem solving)
- Activities: 3 course, 6 extra
-
2x-10x tables
- Activities: 5 course, 7 extra
-
-
18 learning outcomes – click to view
3.OA.2 – Interpret whole-number quotients of whole numbers, e.g., interpret 56 ÷ 8 as the number of objects in each share when 56 objects are partitioned equally into 8 shares, or as a number of shares when 56 objects are partitioned into equal shares of 8 objects each. For example, describe a context in which a number of shares or a number of groups can be expressed as 56 ÷ 8.
-
8 learning outcomes – click to view
Samples: Sharing equally. Dividing by 2. Dividing by 2 (problem solving). Using the division symbol. Dividing by 3.
-
Sharing between 2
- Activities: 0 course, 5 extra
-
Dividing by 2
- Activities: 4 course, 1 extra
-
Dividing by 2 (problem solving)
- Activities: 2 course, 3 extra
-
Using the division symbol
- Activities: 3 course, 0 extra
-
Dividing by 3
- Activities: 4 course, 3 extra
-
Dividing by 3 (problem solving)
- Activities: 2 course, 2 extra
-
Dividing by 4
- Activities: 4 course, 3 extra
-
Dividing by 4 (problem solving)
- Activities: 2 course, 4 extra
-
-
8 learning outcomes – click to view
3.OA.3 – Use multiplication and division within 100 to solve word problems in situations involving equal groups, arrays, and measurement quantities, e.g., by using drawings and equations with a symbol for the unknown number to represent the problem. (See Glossary, Table 2. http://www.corestandards.org/the-standards/mathematics/glossary/glossary/ )
-
28 learning outcomes – click to view
Samples: Groups of 2. Groups of 3. Groups of 4. Groups of 5. Groups of 10. Counting on number line (by 2's).
-
Groups of two
- Activities: 4 course, 7 extra
-
Number patterns and groups (of 3)
- Activities: 3 course, 1 extra
-
Groups and rows of 4
- Activities: 3 course, 4 extra
-
Groups of five
- Activities: 5 course, 14 extra
-
Groups of ten
- Activities: 5 course, 6 extra
-
Counting on by two on a number line
- Activities: 7 course, 5 extra
-
Counting on by five on a number line
- Activities: 6 course, 3 extra
-
Counting on by ten on a number line
- Activities: 6 course, 5 extra
-
Groups and rows of 6
- Activities: 2 course, 0 extra
-
Groups and rows of 7
- Activities: 2 course, 0 extra
-
Groups and rows of 8
- Activities: 2 course, 0 extra
-
Groups and rows of 9
- Activities: 2 course, 0 extra
-
Dividing by 2
- Activities: 4 course, 1 extra
-
2x tables (problem solving)
- Activities: 2 course, 7 extra
-
3x tables (problem solving)
- Activities: 3 course, 3 extra
-
4x tables (problem solving)
- Activities: 3 course, 6 extra
-
5x tables (problem solving)
- Activities: 2 course, 6 extra
-
6x tables (problem solving)
- Activities: 2 course, 6 extra
-
7x tables (problem solving)
- Activities: 3 course, 6 extra
-
8x tables (problem solving)
- Activities: 2 course, 5 extra
-
9x tables (problem solving)
- Activities: 3 course, 7 extra
-
10x tables (problem solving)
- Activities: 2 course, 5 extra
-
2x-10x tables (problem solving)
- Activities: 5 course, 8 extra
-
Dividing by 2 (problem solving)
- Activities: 2 course, 3 extra
-
Dividing by 3 (problem solving)
- Activities: 2 course, 2 extra
-
Dividing by 6 (problem solving)
- Activities: 3 course, 4 extra
-
Dividing by 7 (problem solving)
- Activities: 4 course, 3 extra
-
Division facts (problem solving)
- Activities: 1 course, 6 extra
-
-
28 learning outcomes – click to view
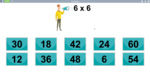
3.OA.4 – Determine the unknown whole number in a multiplication or division equation relating three whole numbers. For example, determine the unknown number that makes the equation true in each of the equations 8 × ? = 48, 5 = _ ÷ 3, 6 × 6 = ?
-
9 learning outcomes – click to view
Samples: 2x-10x tables (missing number). Identifying the dividend. Groups of 2. Groups of 5. Groups of 10. Groups of 3.
-
2x-10x tables (missing number)
- Activities: 3 course, 12 extra
-
Dividing two-digits by one-digit (missing number)
- Activities: 3 course, 2 extra
-
2x tables
- Activities: 12 course, 6 extra
-
5x tables
- Activities: 9 course, 7 extra
-
10x tables
- Activities: 9 course, 6 extra
-
3x tables
- Activities: 8 course, 8 extra
-
4x tables
- Activities: 9 course, 6 extra
-
Dividing by 3
- Activities: 4 course, 3 extra
-
Dividing by 4
- Activities: 4 course, 3 extra
-
-
9 learning outcomes – click to view
Mathematics
3.OA.5 – Apply properties of operations as strategies to multiply and divide. (Students need not use formal terms for these properties.) Examples If 6 × 4 = 24 is known, then 4 × 6 = 24 is also known. (Commutative property of multiplication.) 3 × 5 × 2 can be found by 3 × 5 = 15, then 15 × 2 = 30, or by 5 × 2 = 10, then 3 × 10 = 30. (Associative property of multiplication.) Knowing that 8 × 5 = 40 and 8 × 2 = 16, one can find 8 × 7 as 8 × (5 + 2) = (8 × 5) + (8 × 2) = 40 + 16 = 56. (Distributive property.)
3.OA.6 – Understand division as an unknown-factor problem. For example, find 32 ÷ 8 by finding the number that makes 32 when multiplied by 8.
-
2 learning outcomes – click to view
Samples: Identifying the dividend. 2x-10x tables (missing number). Dividing two-digits by one-digit (missing number).
-
Dividing two-digits by one-digit (missing number)
- Activities: 3 course, 2 extra
-
2x-10x tables (missing number)
- Activities: 3 course, 12 extra
-
-
2 learning outcomes – click to view
Mathematics
3.OA.7 – Fluently multiply and divide within 100, using strategies such as the relationship between multiplication and division (e.g., knowing that 8 × 5 = 40, one knows 40 ÷ 5 = 8) or properties of operations. By the end of Grade 3, know from memory all products of two one-digit numbers.
-
19 learning outcomes – click to view
Samples: Groups of 2. Groups of 3. Challenge Puzzle - 3x tables. Groups of 4. 4x Multiplication facts - puzzle. Groups of 5.
-
2x tables
- Activities: 12 course, 6 extra
-
3x tables
- Activities: 8 course, 8 extra
-
Puzzle - 3x tables
- Activities: 1 course, 0 extra
-
4x tables
- Activities: 9 course, 6 extra
-
4x tables - puzzle
- Activities: 1 course, 0 extra
-
5x tables
- Activities: 9 course, 7 extra
-
6x tables
- Activities: 7 course, 4 extra
-
7x tables
- Activities: 7 course, 5 extra
-
8x tables
- Activities: 7 course, 5 extra
-
9x tables
- Activities: 7 course, 6 extra
-
2x-10x tables
- Activities: 5 course, 12 extra
-
Dividing by 3
- Activities: 4 course, 3 extra
-
Dividing by 4
- Activities: 4 course, 3 extra
-
Dividing by 6
- Activities: 2 course, 1 extra
-
Dividing by 7
- Activities: 2 course, 1 extra
-
Dividing by 8
- Activities: 2 course, 1 extra
-
Dividing by 9
- Activities: 2 course, 1 extra
-
2x-10x tables - puzzle
- Activities: 1 course, 0 extra
-
Dividing two-digits by one-digit (no remainders)
- Activities: 8 course, 8 extra
-
-
19 learning outcomes – click to view
Mathematics
3.OA.8 – Solve two-step word problems using the four operations. Represent these problems using equations with a letter standing for the unknown quantity. Assess the reasonableness of answers using mental computation and estimation strategies including rounding. (This standard is limited to problems posed with whole numbers and having whole-number answers; students should know how to perform operations in the conventional order when there are no parentheses to specify a particular order.)
-
5 learning outcomes – click to view
Samples: Subtraction (two step problem solving). Represent problems using algebraic equation. Two step problem solving.
-
Subtraction (two step problem solving)
- Activities: 2 course, 1 extra
-
Represent problems using algebraic equation
- Activities: 1 course, 0 extra
-
Two step problem solving
- Activities: 1 course, 1 extra
-
Two step problem solving
- Activities: 1 course, 0 extra
-
Two step problem solving
- Activities: 1 course, 0 extra
-
-
5 learning outcomes – click to view
3.OA.9 – Identify arithmetic patterns (including patterns in the addition table or multiplication table), and explain them using properties of operations. For example, observe that 4 times a number is always even, and explain why 4 times a number can be decomposed into two equal addends.
-
9 learning outcomes – click to view
Samples: Groups of 6. Rows of 7. Groups of 8. Groups of 9. Number Patterns (2,3,5,10).
-
Groups and rows of 6
- Activities: 2 course, 0 extra
-
Groups and rows of 7
- Activities: 2 course, 0 extra
-
Groups and rows of 8
- Activities: 2 course, 0 extra
-
Groups and rows of 9
- Activities: 2 course, 0 extra
-
Number Patterns (2,3,5,10)
- Activities: 2 course, 5 extra
-
Representing word problems as number sentences
- Activities: 1 course, 0 extra
-
Number patterns - Identifying the rule
- Activities: 2 course, 0 extra
-
Continue number patterns resulting from addition or subtraction
- Activities: 1 course, 1 extra
-
Shapes Algebra
- Activities: 2 course, 0 extra
-
-
9 learning outcomes – click to view
3.NBT – Number & Operations in Base Ten
Mathematics
3.NBT.1 – Use place value understanding to round whole numbers to the nearest 10 or 100.
-
2 learning outcomes – click to view
Samples: Rounding to the nearest 10 (3 digits). Rounding to the nearest hundred. Rounding numbers: Activity 2.
-
Rounding to the nearest 10
- Activities: 3 course, 3 extra
-
Rounding to the nearest hundred
- Activities: 3 course, 0 extra
-
-
2 learning outcomes – click to view
3.NBT.2 – Fluently add and subtract within 1000 using strategies and algorithms based on place value, properties of operations, and/or the relationship between addition and subtraction.
-
7 learning outcomes – click to view
Samples: Adding three digit numbers using blocks. Subtracting 10 large numbers. Subtracting 100.
-
Place value - adding three-digit numbers
- Activities: 2 course, 0 extra
-
Subtracting 10 from larger numbers
- Activities: 1 course, 1 extra
-
Subtracting 100 from larger numbers
- Activities: 1 course, 1 extra
-
Place value - subtracting three-digit numbers
- Activities: 1 course, 0 extra
-
Subtracting from 1000
- Activities: 6 course, 12 extra
-
Subtraction - missing number
- Activities: 1 course, 2 extra
-
Subtraction and addition (problem solving)
- Activities: 1 course, 1 extra
-
-
7 learning outcomes – click to view
3.NBT.3 – Multiply one-digit whole numbers by multiples of 10 in the range 10–90 (e.g., 9 × 80, 5 × 60) using strategies based on place value and properties of operations.
-
4 learning outcomes – click to view
Samples: Multiplying multiples of 10 by a single digit. Challenge Puzzle. Short multiplication of multiples of 10.
-
Multiplying a single-digit number by multiples of 10
- Activities: 8 course, 5 extra
-
Multiplying multiples of 10 - puzzle
- Activities: 1 course, 0 extra
-
Multiples of 10 by 1 digit - problem solving
- Activities: 0 course, 1 extra
-
Multiplying a two-digit number by a one-digit number - problem solving
- Activities: 5 course, 7 extra
-
-
4 learning outcomes – click to view
3.NF – Number & Operations—Fractions¹ (Grade 3 expectations in this domain are limited to fractions with denominators 2, 3, 4, 6, 8.)
Mathematics
3.NF.1 – Understand a fraction 1/b as the quantity formed by 1 part when a whole is partitioned into b equal parts; understand a fraction a/b as the quantity formed by a parts of size 1/b.
-
6 learning outcomes – click to view
Samples: A half. Halving groups. Representing fractions. Writing fractions. Identifying Fractions. Counting on - fractions. A half.
-
Halving objects
- Activities: 4 course, 4 extra
-
Halving groups
- Activities: 3 course, 1 extra
-
Fractions (problem solving)
- Activities: 1 course, 0 extra
-
Identifying fractions
- Activities: 6 course, 4 extra
-
Identifying mixed fractions
- Activities: 1 course, 0 extra
-
Counting by fractions
- Activities: 1 course, 0 extra
-
-
6 learning outcomes – click to view
3.NF.2 – Understand a fraction as a number on the number line; represent fractions on a number line diagram.
3.NF.2.a – Represent a fraction 1/b on a number line diagram by defining the interval from 0 to 1 as the whole and partitioning it into b equal parts. Recognize that each part has size 1/b and that the endpoint of the part based at 0 locates the number 1/b on the number line.
-
1 learning outcomes – click to view
Samples: Fractions on a number line. Fractions on a number line (with guides). Fractions on a number line.
-
Fractions on a number line.
- Activities: 4 course, 1 extra
-
-
1 learning outcomes – click to view
3.NF.2.b – Represent a fraction a/b on a number line diagram by marking off a lengths 1/b from 0. Recognize that the resulting interval has size a/b and that its endpoint locates the number a/b on the number line.
-
1 learning outcomes – click to view
Samples: Fractions on a number line. Fractions on a number line (with guides). Fractions on a number line.
-
Fractions on a number line.
- Activities: 4 course, 1 extra
-
-
1 learning outcomes – click to view
3.NF.3 – Explain equivalence of fractions in special cases, and compare fractions by reasoning about their size.
3.NF.3.a – Understand two fractions as equivalent (equal) if they are the same size, or the same point on a number line.
-
4 learning outcomes – click to view
Samples: Modelling equivalent fractions. Equivalent Fractions. Hundredths In Their Lowest Form.
-
Modelling equivalent fractions
- Activities: 3 course, 3 extra
-
Equivalent fractions - fraction models
- Activities: 2 course, 0 extra
-
Hundredths in their lowest forms
- Activities: 2 course, 0 extra
-
Comparing fractions as quantities.
- Activities: 2 course, 0 extra
-
-
4 learning outcomes – click to view
3.NF.3.b – Recognize and generate simple equivalent fractions, e.g., 1/2 = 2/4, 4/6 = 2/3). Explain why the fractions are equivalent, e.g., by using a visual fraction model.
-
2 learning outcomes – click to view
Samples: Equivalent Fractions. Modelling equivalent fractions. Matching equivalent fractions using fraction models.
-
Equivalent fractions - fraction models
- Activities: 2 course, 0 extra
-
Modelling equivalent fractions
- Activities: 3 course, 3 extra
-
-
2 learning outcomes – click to view
3.NF.3.c – Express whole numbers as fractions, and recognize fractions that are equivalent to whole numbers. Examples: Express 3 in the form 3 = 3/1; recognize that 6/1 = 6; locate 4/4 and 1 at the same point of a number line diagram.
-
10 learning outcomes – click to view
Samples: Introduction to Fractions. Quarters. Fractions of groups. Representing fractions. Writing fractions.
-
Halves, thirds and quarters
- Activities: 2 course, 1 extra
-
Halves, quarters and eighths
- Activities: 7 course, 9 extra
-
Dividing groups into halves and quarters
- Activities: 5 course, 5 extra
-
Fractions (problem solving)
- Activities: 1 course, 0 extra
-
Identifying fractions
- Activities: 6 course, 4 extra
-
Identifying mixed fractions
- Activities: 1 course, 0 extra
-
Equivalent fractions - fraction models
- Activities: 2 course, 0 extra
-
Comparing fractions as quantities.
- Activities: 2 course, 0 extra
-
Modelling equivalent fractions
- Activities: 3 course, 3 extra
-
Comparing fractions to one whole
- Activities: 1 course, 0 extra
-
-
10 learning outcomes – click to view
3.NF.3.d – Compare two fractions with the same numerator or the same denominator by reasoning about their size. Recognize that comparisons are valid only when the two fractions refer to the same whole. Record the results of comparisons with the symbols >, =, or <, and justify the conclusions, e.g., by using a visual fraction model.
-
2 learning outcomes – click to view
Samples: ComparingFractionsAsQuantities. Modelling equivalent fractions. Comparing fractions as quantities.
-
Comparing fractions as quantities.
- Activities: 2 course, 0 extra
-
Modelling equivalent fractions
- Activities: 3 course, 3 extra
-
-
2 learning outcomes – click to view
3.MD – Measurement & Data
Mathematics
3.MD.1 – Tell and write time to the nearest minute and measure time intervals in minutes. Solve word problems involving addition and subtraction of time intervals in minutes, e.g., by representing the problem on a number line diagram.
-
5 learning outcomes – click to view
Samples: Estimate the duration of time. Months of the Year. Reading a Calendar. Timelines. Telling the time.
-
Most likely duration for an event
- Activities: 1 course, 2 extra
-
Months of the Year
- Activities: 1 course, 3 extra
-
Reading a Calendar
- Activities: 2 course, 5 extra
-
Timelines
- Activities: 1 course, 5 extra
-
Reading Time - to the minute
- Activities: 4 course, 11 extra
-
-
5 learning outcomes – click to view
3.MD.2 – Measure and estimate liquid volumes and masses of objects using standard units of grams (g), kilograms (kg), and liters (l). (Excludes multiplicative comparison problems (problems involving notions of “times as much”; see Glossary, Table 2 http://www.corestandards.org/the-standards/mathematics/glossary/glossary/ ). Add, subtract, multiply, or divide to solve one-step word problems involving masses or volumes that are given in the same units, e.g., by using drawings (such as a beaker with a measurement scale) to represent the problem. (Excludes compound units such as cm3 and finding the geometric volume of a container.)
-
8 learning outcomes – click to view
Samples: Comparing volume (empty to full). Measuring capacity using informal units tutorial.
-
Full to empty
- Activities: 3 course, 1 extra
-
Direct comparison - volume
- Activities: 1 course, 4 extra
-
Volume using informal units
- Activities: 3 course, 10 extra
-
Objects using cubes
- Activities: 3 course, 5 extra
-
Measure volume using litres and milliltres
- Activities: 1 course, 6 extra
-
Measure mass in grams and kilograms
- Activities: 1 course, 13 extra
-
Compare mass using a balance scale
- Activities: 4 course, 2 extra
-
Measure mass with informal units
- Activities: 5 course, 7 extra
-
-
8 learning outcomes – click to view
Mathematics
3.MD.3 – Draw a scaled picture graph and a scaled bar graph to represent a data set with several categories. Solve one- and two-step “how many more” and “how many less” problems using information presented in scaled bar graphs. For example, draw a bar graph in which each square in the bar graph might represent 5 pets.
-
6 learning outcomes – click to view
Samples: Data tables. Data - tally marks. Interpret data in lists. Data - picture graphs. Create a Column Graph. Data.
-
Interpret data presented in a table
- Activities: 3 course, 3 extra
-
Interpret data presented with tally marks
- Activities: 2 course, 2 extra
-
Interpret data presented in lists
- Activities: 1 course, 0 extra
-
Interpret data presented using picture graphs.
- Activities: 2 course, 4 extra
-
Data & Graphs - Column Graph Creator
- Activities: 0 course, 1 extra
-
Interpret data presented using simple column graphs
- Activities: 0 course, 6 extra
-
-
6 learning outcomes – click to view
3.MD.4 – Generate measurement data by measuring lengths using rulers marked with halves and fourths of an inch. Show the data by making a line plot, where the horizontal scale is marked off in appropriate units— whole numbers, halves, or quarters.
Mathematics
3.MD.5 – Recognize area as an attribute of plane figures and understand concepts of area measurement.
3.MD.5.a – A square with side length 1 unit, called “a unit square,” is said to have “one square unit” of area, and can be used to measure area.
-
2 learning outcomes – click to view
Samples: Counting by using rows. Area using square tiles. Counting by using rows. Partitioned rectangles.
-
Partitioned rectangles
- Activities: 3 course, 0 extra
-
Area using square tiles
- Activities: 1 course, 0 extra
-
-
2 learning outcomes – click to view
3.MD.5.b – A plane figure which can be covered without gaps or overlaps by n unit squares is said to have an area of n square units.
-
2 learning outcomes – click to view
Samples: Area using informal units. Counting by using rows. Area using informal units. Counting by using rows.
-
Area using informal units.
- Activities: 2 course, 5 extra
-
Partitioned rectangles
- Activities: 3 course, 0 extra
-
-
2 learning outcomes – click to view
3.MD.6 – Measure areas by counting unit squares (square cm, square m, square in, square ft, and improvised units).
-
1 learning outcomes – click to view
Samples: Measure using square centimetres. Measure using square centimetres. Measure area using a grid tutorial.
-
Area using a grid.
- Activities: 4 course, 10 extra
-
-
1 learning outcomes – click to view
3.MD.7 – Relate area to the operations of multiplication and addition.
3.MD.7.a – Find the area of a rectangle with whole-number side lengths by tiling it, and show that the area is the same as would be found by multiplying the side lengths.
-
2 learning outcomes – click to view
Samples: Counting by using rows. Area using square tiles. Counting by using rows. Partitioned rectangles.
-
Partitioned rectangles
- Activities: 3 course, 0 extra
-
Area using square tiles
- Activities: 1 course, 0 extra
-
-
2 learning outcomes – click to view
3.MD.7.b – Multiply side lengths to find areas of rectangles with whole-number side lengths in the context of solving real world and mathematical problems, and represent whole-number products as rectangular areas in mathematical reasoning.
-
1 learning outcomes – click to view
Samples: Calculating area. Area of Squares and Rectangles. Calculating the area of squares and rectangles. Calculating Area.
-
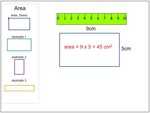
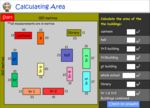
Calculating area (squares and rectangles)
- Activities: 5 course, 9 extra
-
-
1 learning outcomes – click to view
3.MD.7.c – Use tiling to show in a concrete case that the area of a rectangle with whole-number side lengths a and b + c is the sum of a × b and a × c. Use area models to represent the distributive property in mathematical reasoning.
-
3 learning outcomes – click to view
Samples: Area using square tiles. Measure using square centimetres. Calculating area. Measure using square centimetres.
-
Area using square tiles
- Activities: 1 course, 0 extra
-
Area using a grid.
- Activities: 4 course, 10 extra
-
Square centimetres
- Activities: 2 course, 8 extra
-
-
3 learning outcomes – click to view
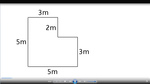
3.MD.7.d – Recognize area as additive. Find areas of rectilinear figures by decomposing them into non-overlapping rectangles and adding the areas of the non-overlapping parts, applying this technique to solve real world problems.
-
2 learning outcomes – click to view
Samples: Calculating the Area of Irregular Shapes. Calculating the Area of Irregular Shapes. Area of irregular shapes.
-
Area of irregular shapes
- Activities: 3 course, 1 extra
-
Calculate the area of irregular shapes.
- Activities: 0 course, 3 extra
-
-
2 learning outcomes – click to view
Mathematics
3.MD.8 – Solve real world and mathematical problems involving perimeters of polygons, including finding the perimeter given the side lengths, finding an unknown side length, and exhibiting rectangles with the same perimeter and different areas or with the same area and different perimeters.
-
3 learning outcomes – click to view
Samples: Perimeter. Perimeter of irregular shapes. Perimeter and Area. Perimeter of squares and rectangles.
-
Perimeter of squares and rectangles.
- Activities: 3 course, 4 extra
-
Perimeter of irregular shapes.
- Activities: 3 course, 9 extra
-
Perimeter and Area
- Activities: 1 course, 0 extra
-
-
3 learning outcomes – click to view
3.G – Geometry
Mathematics
3.G.1 – Understand that shapes in different categories (e.g., rhombuses, rectangles, and others) may share attributes (e.g., having four sides), and that the shared attributes can define a larger category (e.g., quadrilaterals). Recognize rhombuses, rectangles, and squares as examples of quadrilaterals, and draw examples of quadrilaterals that do not belong to any of these subcategories.
-
4 learning outcomes – click to view
Samples: Tessellating patterns. Identifying types of lines. Shapes. Constructing 2D shapes. Tessellating patterns.
-
Identifying shapes based on attributes
- Activities: 4 course, 0 extra
-
Identifying types of lines
- Activities: 2 course, 2 extra
-
Describe two dimensional shapes
- Activities: 0 course, 1 extra
-
Construct and draw two dimensional shapes
- Activities: 3 course, 3 extra
-
-
4 learning outcomes – click to view
3.G.2 – Partition shapes into parts with equal areas. Express the area of each part as a unit fraction of the whole. For example, partition a shape into 4 parts with equal area, and describe the area of each part as 1/4 of the area of the shape.
-
6 learning outcomes – click to view
Samples: Fractions of an area. Identifying Fractions. Equivalent Fractions. ComparingFractionsAsQuantities.
-
Fractions of an area
- Activities: 1 course, 1 extra
-
Identifying mixed fractions
- Activities: 1 course, 0 extra
-
Equivalent fractions - fraction models
- Activities: 2 course, 0 extra
-
Comparing fractions as quantities.
- Activities: 2 course, 0 extra
-
Hundredths in their lowest forms
- Activities: 2 course, 0 extra
-
Halves, quarters and eighths
- Activities: 7 course, 9 extra
-
-
6 learning outcomes – click to view