Fullscreen
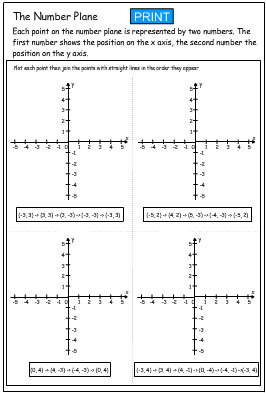
Coordinate Quadrants Draw Shapes
- Grade: Year 6
Activity type: Printable

Sorry your device is unable to run Adobe Flash Activities
You can play any activities that do not have the Flash Symbol while on this device.
For help on making these flash activites work try our help page.
You can play any activities that do not have the Flash Symbol while on this device.
For help on making these flash activites work try our help page.

Please Note: This activity needs Adobe Flash Player to run.
Students with Tablets that cannot run Adobe flash will not be able to play this activity.
Students with Tablets that cannot run Adobe flash will not be able to play this activity.
To save results or sets tasks for your students you need to be logged in. Join Now, Free
Coordinate Quadrants Draw Shapes
- Course
Mathematics - Grade
Year 6 - Section
Location and Transformation - Outcome
Cartesian Planes - Activity Type
Printable - Activity ID
20540
