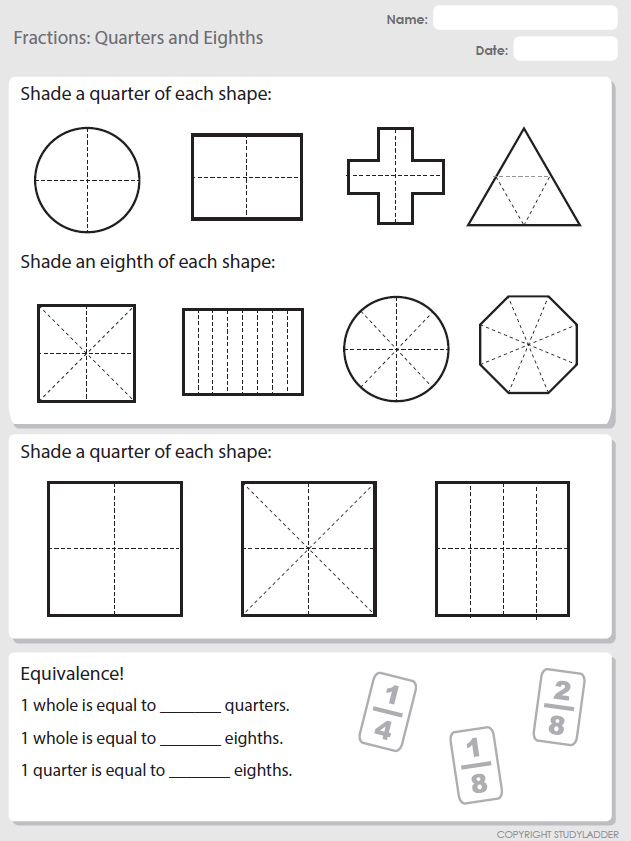
Quarters and eighths
- Grade: All grades
Activity type: Printable
To save results or sets tasks for your students you need to be logged in. Join Now, Free
Quarters and eighths
- Course
Mathematics - Grade
n.a. - Section
Printable Worksheets - Outcome
Fractions - Activity Type
Printable - Activity ID
3776